Future Development of Quantum Computing and Its Relevance to NATO
Publication Type:
Journal ArticleSource:
Connections: The Quarterly Journal, Volume 20, Issue 2, p.89-109 (2021)Keywords:
complexity theory, cryptography, NATO, Quantum computing, quantum cybersecurity, quantum key distribution, quantum resilience, quantum supremacyAbstract:
The first quantum computers are becoming a reality, and scientists working in various areas look forward to taking advantage of their enormous computational potential. At the same time, the high performance of quantum computers imposes serious risks for cybersecurity. We can expect an arms race between rival parties: a defensive side trying to ensure the privacy and dependability of stored and transmitted information and their adversaries. With this article, the authors aim to provide an overview of the status of quantum computer development, project the next steps, and investigate the impact future quantum systems may have on cybersecurity and military operations. We first discuss the basic aspects that differentiate quantum computing from classical computing and find that analogies between both domains are quite limited. The world of quantum computers is remarkably diverse already, and we elaborate that quantum simulators and universal quantum computers have “qubits” in common but still work in fundamentally different ways. Since security experts focus on upcoming trends in quantum computing, we take a look at the latest technologies and at the race for first reaching “quantum supremacy.” Finally, we provide a detailed analysis of the specific risks future quantum computers represent for established cryptosystems and conclude that asymmetric algorithms like the RSA protocol are particularly vulnerable. The dangers of quantum computing for cryptography are obvious, as is the high relevance of the safety of stored and transmitted data to the defense sector. However, we examine the capability spectrum of quantum technologies and discover that breaking asymmetric encryption algorithms is just one facet, and other features like Grover’s quantum algorithm may revolutionize the logistics of the armed forces. Satellite Quantum Key Distribution is another promising concept that may change the communication between military units. To NATO, quantum computing is a double-edged sword: the alliance needs to use the developments to benefit from the potential and be ready to counter the cyber threats. We derive ideas of what NATO should do in order to prepare for the quantum era.
Introduction
Already in our era of “classical computing,” maintaining cybersecurity is an enormous challenge. After the 2007 cyberattacks on Estonia, in 2008, NATO adopted for the first time a “Cyber Defense Policy” and established the “Cyber Defense Management Authority” in Brussels.[1] NATO’s 2010 “Strategic Concept” acknowledges the importance of hybrid threats, including cyberattacks, as complex risks characterized by not being confined by geographical limits.
For the financial industry, in particular, the perils of cyberspace are assuming alarming proportions. CyberSecurity Ventures and IBM report that ransomware attacks on newcomers to the field occur every 14 seconds. In 2016, 64 % more cyberattacks targeted the finance sector than other sectors.[2] Man-in-the-middle attacks, i.e., the interception or manipulation of communications between two parties, represent a particular risk for financial but also for other sectors. Therefore, it is recommended that companies and agencies protect all access points by implementing a range of security measures.[3]
Since defensive technologies have improved, successful cyberattacks on corporate, government, or military networks increasingly require the resources of larger government or criminal organizations. The analysis of the sources of cyberattacks reveals that while many assaults on financial institutions are still carried out by small group threat actors attempting to extort money, exploitation activities aimed at government or military targets are primarily operations at the nation-state level.[4]
Even advanced digital infrastructure protection may soon be insufficient because the availability of quantum computers will mean a new quality of cyberattacks. According to a group of economic heavyweights, including Microsoft and JPMorgan, a quantum computer of commercial relevance will be on the market by 2030, possibly as soon as 2024.[5] The worldwide market for quantum computing is predicted to be more than USD 10 billion by 2024.[6]
Such predictions are questioned by many experts, however. Invoking the need for many technical advancements, they estimate that it will take several decades to build quantum computers with the ability to crack presently used cryptosystems, and they do not rule out that such attempts may not be successful at all. Therefore, these experts are convinced that quantum computers posing a threat to established cryptography methods will not be available by 2030.[7] Nevertheless, managers of databases storing sensitive information with a need for long-term protection, such as classified government documents or long-dated root certificates, should look for alternatives to asymmetric algorithms.[8]
The expected upheaval of cryptosystems induced by quantum computing and the significance of cryptography for military operations suggest that NATO needs to begin preparing the relevant systems for quantum cyber attacks already now. However, cryptography is by no means the only field that quantum technologies will revolutionize, and some sectors, like long-distance communication, are also of high relevance to NATO. In this article, we will take a closer look at possible scenarios.
The remainder of this article is organized as follows: In Section II a, we discuss what sets the quantum computer apart from the classical computer. Section II b takes a look at the different types of quantum computers. Section II c examines aspects of quantum computing technology, and Section II d provides information on the term “quantum supremacy.” Section III analyses the difficulties of predicting the future of quantum computing. Section IV gives an overview of the problem-solving abilities of quantum computers. Section V takes a look at the impact of quantum computing on cybersecurity in general. Section VI studies how quantum skills are touching military issues and the results of our research are summarized in Section VII.
II. Science and Technology of Quantum Computing
a. Classical vs. Quantum Computer
Let us first take a look at the differences between “classical” and “quantum” computers. In classical computers, “bits,” which can take the values zero or one (“binary system”), are represented by electrical signals, and data are processed in the form of a linear stream of bits. The classical bit is replaced by the “quantum bit” or “qubit” in quantum computers, and a qubit corresponds to a particle, e.g., photon or electron, not to an electrical signal. Quantum computing is of great interest because a small number of qubits already allows for the storage and processing of enormous amounts of data.
Similar to a bit, a qubit can also be found in one of two states upon measurement, e.g., spin up or spin down (in quantum mechanics, the spin of a particle is an intrinsic form of angular momentum). So what is the big difference between classical and quantum computing? In a classical computer, information is processed in a linear mode, and in an exponential mode in a quantum computer. The physical explanations for this distinction are that microscopic objects can be in “superposition” states (before observation, the spin state of an electron can be “up,” “down,” or a superposition of both) and that the collective state of a combined system of several microscopic objects can be a superposition of the individual states of these objects (“entanglement”).
“Entanglement” and “superposition” are only possible for quantum states, not for classical states. In a quantum computer, an ensemble of entangled qubits is prepared so that the coherent system is in a superposition of all combinatorial qubit configurations before measurement. Entanglement makes the programming of multi-qubit logical gates possible.[9] The coherence time is defined as the time quantum states can be used for technology.[10]
Let us consider the “knowledge” of an observer about a quantum mechanical system. There is a fundamental difference between the instants of time “before measurement” and “after measurement” because quantum mechanics is a statistical theory. Depending on the number of entangled qubits, the multitude of potential outcomes of the observation, which corresponds to the possible computation results, can be enormous. The “calculation,” i.e., the measurement, selects just a random single configuration of entangled qubit states out of the plenitude of possible test readings.
The randomness of the result of a single observation is due to the probabilistic nature of quantum mechanics. Quantum indeterminacy means that an undisturbed qubit can represent any value allowed by the superposition of states.[11] Without manipulation, the measurement results spin up and down are equally likely. However, each outcome is associated with an individual probability amplitude. Quantum computing corresponds to a manipulation of a qubit so that the chance to observe the preferred outcome, say spin up, is increased.[12] The trick will be to arrange the qubits so that the probability of a correct and a wrong answer is maximized and minimized, respectively. The experiment needs to be repeated until a sufficient sample size ensures the statistical significance of the mean result is reached.
Due to the entanglement of qubits, the measurement process in quantum computing can “create” information content that increases exponentially with the number of qubits. The qubit configuration selection step, which exploits the wave nature of quantum mechanical states, can be interpreted as the realization of a processor performing as many operations as there are possible qubit configurations at the same time. This feature is responsible for the predicted high efficiency of quantum computers in answering specific “quantum-adapted” mathematical questions.
Quantum processors are therefore not generally “faster” than classical processors in solving any type of computational problem, e.g., because they would perform more clock cycles per time unit, in the same way as the speed of classical processors is defined. Quantum processors can only outpace classical processors if the computational task can be cast in a form that allows for the utilization of the quantum mechanical wave properties of qubits. Suppose a system of entangled qubits can be arranged to selectively amplify the solution to a mathematical problem and cancel all qubit configurations corresponding to wrong answers via destructive phase interferences. In that case, a quantum processor can obtain a result much quicker than a classical processor because the required number of quantum operations (“measurements”) is much smaller than the number of classical floating-point operations.[13]
b. Two Types of Quantum Computers
In the previous section, we generally referred to the “quantum computer,” however, we need to be more precise about the terminology we are using here. In this section, we provide definitions (as far as possible) of different forms of quantum computing. When we mentioned the programming of multi-qubit logical gates in the previous section, we implicitly described a property of the “universal quantum computer.” However, many other features are true for both the “quantum simulator” and the “universal quantum computer,” the two main classes of quantum computers.
The first type of quantum computer is the quantum simulator or quantum emulator. Quantum simulators can be viewed to some extent as analog systems designed to study specific quantum phenomena that are difficult to investigate experimentally and too complex for simulation with a classical supercomputer. Quantum simulators take advantage of the quantum mechanical properties of superposition and entanglement. They have been implemented in the form of different physical systems, e.g., as trapped-ion simulators or ultracold atom simulators.
Quantum annealing can be described as an analog version of quantum computing,[14] although quantum annealers can be dynamically configured (“programmed”) using software.[15] These quantum processors employ qubits that have minimal entanglement but allow for coherence times that are sufficiently long to complete the calculation.
Quantum annealers can be interpreted as quantum simulators using superconducting qubits to determine the ground states of Hamiltonians of spin systems by adiabatically ramping an external magnetic field from an initial to a final value. The Hamiltonian is a mathematical operator defining the energy levels of a quantum mechanical system. The term “adiabatic” implies that the external field is applied in a way so that the system eigenfunctions (the quantized stationary states of the system) change slowly and the occupation numbers of the states remain unchanged. Various profiles of an adiabatic ramp can be designed to adiabatically transform the initial to the final Hamiltonian. The ground state of this final problem Hamiltonian corresponds to the solution.[16] This approach takes advantage of quantum mechanical tunneling through potential barriers to investigate the topology of the energy surface.[17]
Quantum annealers are specifically designed to find the global minimum of a function with many local minima. This corresponds to tackling combinatorial optimization tasks like the Travelling Salesman Problem (TSP), i.e., problems distinguished by a discrete search space. The computational mode of quantum annealers is based on quantum fluctuations and not on the manipulation (controlled, non-random entanglement) of qubits.
The first commercial quantum annealer was launched in 2011 by D-Wave Systems. A speedup by a factor of 108 on a set of hard optimization problems was reported in 2015 for the D-Wave 2X system as compared to the simulated annealing and quantum Monte Carlo methods.[18] In the D-wave Advantage Pegasus P16 system, released in 2020, the quantum annealing principle is used for calculations involving more than five thousand randomly entangled, superconducting qubits. This D-wave adiabatic quantum annealer can, e.g., be used for drug discovery.[19] The question of whether quantum annealers really yield advantages for solving certain optimization algorithms over classical computers remains open, though.[20]
The second type of quantum computer is the universal quantum computer. However, there is no unique definition of such a device.[21] According to Krupansky,[22] a universal quantum computer disposes of a sufficiently large number of qubits to solve nontrivial, general problems and can therefore be differentiated from special-purpose and fixed-function quantum computers, which are developed to address certain well defined computational tasks, i.e., from quantum simulators. In other words, what makes a quantum computer universal is a digital-processing layer that converts microinstructions into pulses for the manipulation of qubits, allowing them to perform as quantum logic gates.[23] In this way, all operations on a single qubit or pair of qubits can be carried out.
Since “digital” means “discrete value,” it should be mentioned that also attempts at continuous-variable quantum computing are underway, e.g., Xanadu’s optical computing project.[24]
As described by Krupansky,[25] universal quantum computers are classified according to four levels. A level 1, the quantum computer is a universal quantum Turing machine and cannot execute complex instruction sets. The abilities of the universal quantum computer classes increase at each level to finally reach level 4, characterized by quantum computers that significantly exceed the capacity and performance of a classical computer. A prerequisite to building a level 4 universal quantum computer is the entanglement of a large number of qubits during the entire time of computing, an extreme challenge.
c. Quantum Computing Technology
Due to the possibilities, the interest of science and industry in building quantum computers is enormous, but the same is true for the fundamental and technological requirements. One main problem in realizing a quantum computer is the volatility of entanglement. For a quantum processor to work, it is necessary to keep a certain number of qubits in a superposition of states for a sufficiently long period, i.e., the coherence time. The inherent instability of quantum states leads to the tendency to rapidly dissipate a carefully arranged entanglement, a process called decoherence.
Since the decoherence of qubits is enhanced by external disturbances, a quantum computer must be isolated from the environment. Vacuum containers and very low temperatures are preferred conditions for quantum processors because they are conducive to the stability of qubit superposition and entanglement.[26]
A variety of concepts for the realization of qubits is presently under investigation: superconducting, ion trap, quantum dot, topological, spin-based, and flip-flop. Some are in a very early stage of development, and some are at a more advanced level. Quantum simulators using superconducting qubits are ready for the market. However, a qubit system that would allow for the construction of a universal quantum computer has yet to be discovered.
d. Quantum Supremacy
An important term in the context of describing the status of quantum computing development is “quantum supremacy.” Although a quantum computer able to decipher asymmetric encryption (a so-called “quantum prime computer”) may still be science fiction, some experts believe that another important step in quantum computing may be close: quantum supremacy.[27] Quantum supremacy will be reached once a quantum computer can solve a problem, as artificially as it may be, that cannot be solved by a classical computer in any feasible amount of time.
In October 2019, a team of Google AI Quantum Group and university researchers [28] claimed to have reached quantum supremacy by randomly programming the 53 physical qubits of the “Sycamore” quantum processor, applying both single-qubit and two-qubit logical operations (logic gates).
Because of the instability of physical qubits, certain combinations of physical qubits are required to permit quantum error correction for the derivation of an abstract logical qubit. Quantum error correcting codes represent the information corresponding to the logical state of a single qubit in terms of the entangled state of an ensemble of physical qubits.[29] After quantum error correction for the Sycamore processor, the entangled physical qubits are reduced to a fraction of a single logical qubit.[30]
While in the programming step of a theoretical quantum processor all qubits might be collectively entangled, only adjacent qubits are entangled in the Sycamore. This restriction can, to some degree, be compensated by interchanging qubits, a time-consuming process and therefore detrimental to coherence.[31] Nevertheless, according to Arute and colleagues,[32] the numerical tasks accomplished by the Sycamore processor in ca. 200 seconds would take IBM’s “Summit” supercomputer 10 000 years. IBM immediately challenged the assertion of Arute and colleagues [33] by postulating that upgrading Summit with secondary storage would reduce the time for the simulation of Sycamore circuits down to 2.5 days, sufficiently short to invalidate the Sycamore supremacy statement.[34]
The dispute about the Sycamore quantum supremacy contention yields a foretaste of the challenges for the interpretation and the reliability assessment of quantum computing results that will be imposed by entering a phase characterized by the impossibility to verify these results with conventional supercomputers.[35]
It should not go unmentioned that the rationale of the term “quantum supremacy” has been questioned recently because it would imply the very unlikely scenario that quantum computers might be able to generally outperform classical computers. Instead, future quantum computers are expected to be more efficient than classical computers only at solving specific tasks. Therefore phrases like “quantum advantage” and “quantum practicality” have been suggested to describe the progress in quantum computing.[36]
III. Predicting the Development of Quantum Computing
It is very difficult to forecast the speed of progress in quantum computing. One reason for this uncertainty is the multitude of qubit technologies presently under consideration. In order to decide which qubit architectures will be successful in the long run, many open issues still need to be addressed, both from a theoretical and practical perspective. Another factor is the question of which impact the availability of early generation quantum computers will have on the design of subsequent generations. Finally, it is not easy to figure out on which scale other upcoming innovations like artificial intelligence may also influence the evolution of quantum computers.[37]
In fact, a mutual enhancement of both scientific disciplines is not unlikely since quantum computing will also have an impact on the field of artificial intelligence by performing certain operations much faster than classical computers. This anticipation stimulated the foundation of the interdisciplinary field “Quantum Artificial Intelligence” (QAI). Machine learning is a sub-field of artificial intelligence, and one discipline of QAI is consequently quantum-enhanced machine learning.
A comprehensive study of the potential impact of quantum technologies on political and military interests has been performed by the Institute for Defense Analyses (IDA) for the US Department of Defense in 2019.[38] According to Wolf and colleagues,[39] the development of digital quantum computing will follow three steps: component quantum computation (CQC), noisy intermediate-scale quantum (NISQ) computing, and fault-tolerant quantum computing (FTQC). For superconducting and trapped ions qubits, the NISQ stage has just been reached. Alternative architectures, like quantum dots, are still in the CQC realm. No qubit technology is presently close to the FTQC regime.
Mathematician Peter Shor proposed a quantum computer algorithm for integer factorization in polynomial time in 1994.[40] For the implementation of Shor’s algorithm to factor a number too large for classical supercomputers, an FTQC-level processor integrating ca. 106 physical qubits is required. According to Grumbling and Horowitz, [41] no serious prediction on the availability of such a quantum prime computer can presently be made, but realization will probably take at least 20 years.
It remains to be seen whether Neven’s law, which states that the performance of quantum computers improves at a lightning-fast doubly exponential rate as compared to classical computers, holds up to the reality check. Neven’s law can be interpreted as describing the evolution of qubit numbers in quantum processors in analogy to Moore’s law predicting the number of transistors in conventional processors.[42]
IV. The Suitability of Quantum Computers for Solving Specific Problems
Quantum computers will not generally outperform classical computers in solving problems by a uniform margin. Instead, the advantage of quantum computers over classical computers will depend strongly on the nature of the task to be performed. It has been shown that quantum algorithms have the potential to massively beat classical algorithms in solving a small subset of problems. However, for the solution of many other types of problems, it appears that quantum computers will not make a big difference.[43] Quantum computers can have the edge over classical computers when it comes to finding the global properties of mathematical systems. Still, we will discuss in this section that also, in this case, the improvement of computational efficiency achievable with quantum algorithms depends on the particular nature of the problem.
Before continuing, we need to differentiate between the tasks of finding and of verifying solutions. For decision problems of complexity class P, solutions can be found and verified in polynomial time. Solutions to problems of class “nondeterministic polynomial time” (NP) may not be found in polynomial time but can be verified in polynomial time. Decision problems are referred to as NP-complete if no polynomial-time algorithms, classical or quantum, provide solutions to them that are known.
One example of a “quantum problem” is the decomposition of an n-digit number into prime factors. The solution can obviously be verified in polynomial time. However, with the best-known algorithm for classical computers, the number of steps increases exponentially with n. Therefore, the factoring problem is believed to belong to class NP outside of P. Shor’s quantum algorithm defines the factoring task as a global property of the number and meets this challenge in polynomial time (the algorithm scales with n2).[44] Consequently, the factoring problem is not NP-complete.
However, this performance of Shor’s algorithm does not mean that quantum algorithms will always deliver exponential speedups when it comes to searching for global properties of mathematical systems. A nice example is TSP, which also relates to a global system property. In the first definition of TSP, labeled as TSP1 below, the challenge is to find a route connecting all n nodes of a network that does not exceed the given length L. If S quantifies the number of routes, then S grows exponentially with n. A classical approach will require S/2 attempts on average to find a route matching the condition.
In order to classify the effort for verification of a solution to the TSP, it is important to pay attention to the specific formulation of the puzzle: if it is stated as in TSP1, then verification of the solution can obviously be performed in polynomial time. Grover’s quantum algorithm can identify a connection in ca. S 1/2 steps, which represents a significant improvement as compared to the classical approach but does not reduce exponential scaling to polynomial scaling. This result shows that TSP1 is the same type of problem as searching an unsorted database. Although TSP1 is related to a global property of the network, so far no classical or quantum algorithm solving TSP1 in polynomial time has been discovered, and therefore, TSP1 is believed to be an NP-complete problem.
Another version of TSP is the search for the shortest connection between the n nodes (referred to as TSP2 in the following). In order to answer the question of the minimal route, it is not sufficient to check whether the length of one suggested solution satisfies the condition of undercutting a certain limit. Still, it is required to compare the lengths of all possible paths. Not even a known quantum algorithm can thus verify a solution to TSP2 in polynomial time. TSP2 is probably not NP-complete but belongs to the more comprehensive PSPACE class, which includes problems that can be solved by a classical computer disposing of a polynomial amount of memory but possibly requiring exponential time scaling. PSPACE contains the complexity classes P and NP.[45]
So what differentiates TSP1 from the factoring problem? Shor’s algorithm takes advantage of certain mathematical properties of composite numbers and their factors that can be exploited to realize constructive and destructive interference patterns on a quantum computer, leading to the synthesis of the correct answer. Wrong answers are canceled out via destructive interferences. NP-complete problems like TSP1 appear to not allow for the creation of such interference mechanisms.
When discussing complexity classes, one should keep in mind, though, that no proofs of the nonexistence of quantum or even of classical algorithms for the solution of NP-complete problems have yet been produced. Nevertheless, there is clearly an analogy in the differentiation between classes P and NP on one side and between classes NP and NP-complete on the other. It is believed that P ≠ NP, because no classical algorithms that would be able to solve certain problems, like factoring, in polynomial time, are known. Similarly, it appears likely that NP ≠ NP-complete since no classical or quantum algorithms have yet been discovered that would permit the completion of tasks like TSP1 in polynomial time.
V. Quantum Computing and Security
In our era of classical computing, primarily two classes of encryption algorithms are employed: symmetric and asymmetric. One prominent symmetric protocol is the Advanced Encryption Standard (AES), which supports three key sizes: 128 bits, 192 bits, and 256 bits. The application field of symmetric algorithms is the protection of large amounts of data, e.g., the codification of databases.
Asymmetric encryption employs the so-called public and private keys to encrypt and decrypt data, respectively. The mathematically related keys are generated by cryptographic algorithms that produce so-called one-way functions. A well-known asymmetric approach is the Rivest, Shamir, Adleman (RSA) protocol which exploits the fact that factorization of large bi-prime numbers is too time-consuming for classical computers.[46] Asymmetric methods are slower than symmetric methods but do not require secure channels for exchanging keys if encrypted information is supposed to be shared between two or more parties, as is necessary with symmetric algorithms.[47]
Quantum computing mainly represents a security threat to asymmetric cryptosystems based on prime numbers, e.g., Shor’s quantum algorithm [48] could be used to break RSA encryption, while symmetric protocols are not relying on prime number factorization and are considered to remain safe. A future quantum computer running Shor’s algorithm and powerful enough to compromise a 2048-bit implementation of the RSA protocol in less than a day would not be able to decipher data protected by the AES-128 protocol.[49]
In 1996, computer scientist Lov Kumar Grover presented a quantum algorithm for searching unsorted databases.[50] The database search task corresponds to a situation in which the only way to solve the problem would be to guess the input argument of a black-box function and check the correctness of the output. The Grover method significantly reduces the average number of attempts to find a specific entry in a database with S entries (S corresponds to the size of the function’s domain) to S 1/2 as compared to S/2 with classical computation.
However, the main difficulty in decrypting a symmetric standard like AES is that the size of the database S increases exponentially with the key length. This scaling property is not changed by Grover’s approach. Grover’s algorithm can be applied to decode data encrypted by the AES protocol by searching for a key that matches a small number of plaintext-ciphertext pairs. For example, to decrypt the AES-128 algorithm ca. 265 reversible evaluations of the block cipher need to be performed in serial mode since no efficient parallelization method appears viable and quantum computation of a function is assumed to be more time consuming than classical computation.[51]
The risk induced by today’s extensive use of asymmetric encryption stimulated the development of the so-called “quantum-safe” or “post-quantum” cryptographic algorithms. These protocols are designed for classical computers with the purpose of protecting data against decryption attempts based on quantum computers.[52]
The US Government recently announced that the Commercial National Security Algorithm Suite presently used for data encryption will be replaced by quantum-safe algorithms beginning of 2024, which means that the transition will not be completed until ca. 2030.[53] Since the secrecy of sensitive information needs to be guaranteed for 50 or more years, the US Government obviously does not expect quantum computers able to decrypt, e.g., the RSA-3072 protocol, to become available for several decades.[54]
Nevertheless, advanced quantum-safe functions are currently the subject of intense research. Two public-key cryptosystems that have the potential to replace the RSA protocol are random lattice-based and ideal lattice-based cryptography. The security of these methods originates from the intractability of certain computational problems on random and ideal lattices, respectively. Lattice-based schemes have been shown to yield a large variety of cryptographic tools, some of which are of a completely new type. Included are lattice-based cryptographic algorithms that qualify as post-quantum methods.[55]
Another public-key method is Supersingular Isogeny Diffie-Hellmann Key Exchange (SIDH). SIDH permits the establishment of a secret key between two previously unconversant parties over an otherwise insecure communication channel. By using, with compression, 2688-bit public keys at a 128-bit quantum security level, SIDH employs one of the smallest key sizes of all post-quantum algorithms.[56]
Many investigations also focus on alternatives to quantum-safe cryptography developed for classical computers. One option is Quantum Key Distribution (QKD) which may provide a route to realize unauthenticated key exchange in quantum networking. QKD enables information-theoretically secure encryption, i.e., the cryptosystem cannot be compromised even if a wannabe eavesdropper would dispose of unlimited computing power.[57]
In order to explain this, we briefly have to return to the concepts of quantum indeterminacy and superposition of states that apply to an undisturbed qubit. Observing a quantum particle removes the superposition and implies that the superposition collapses to a single state. This fact can be exploited to ensure the privacy of communication since eavesdropping or man-in-the-middle attacks require a measurement of the particle and consequent termination of the superposition of states. Such surveillance or manipulation attempts can therefore be noticed immediately.[58]
Since the principle enabling QKD is physical in nature and not mathematical, the protection of quantum networks via QKD is not threatened by quantum computers. The high cost means that QKD will only be used for the protection of highly sensitive links in the short term. A future QKD satellite network may allow for the safe global exchange and transport of keys.[59]
However, QKD applications in other cryptography fields beyond quantum networking do not appear very likely because new hardware would be necessary, and costs would be high. According to a white paper released by the UK government in March 2020, [60] significant investments in QKD research are not recommended because of this rather narrow deployment spectrum.[61]
In this article, we have so far concentrated on the function, development, and performance of quantum computing hardware. However, we also need to address the software aspect, particularly programs designed to run on quantum processors. Shor’s and Grover’s algorithms have already been mentioned, and it is clear that it will take many years until both procedures can be implemented on universal quantum computers.
However, the operations of future quantum processors can be simulated on classical computers already now, and prototype quantum devices for testing code are also available. Quantum programming languages are therefore under intense development. For an overview of the present status of this field, we refer the reader to the work of Garhwal and colleagues.[62]
VI. Relevance of Quantum Computers to Military Applications
In a 2012 contribution to the Cicero Foundation’s Great Debate Papers, Estonian security analyst Häly Laasme addressed the opportunities and challenges that quantum computing will mean for NATO.[63] He recommended that: “For NATO to be ready for the quantum era, the discussions concerning the possible technological shift and its consequences should be commenced sooner rather than later, especially considering NATO’s current slow tempo in keeping up with cyber issues.”
Mathematical discoveries like Shor’s algorithm are obviously very important for cryptography. Securing the communications between military units as well as sensitive data, e.g., information on the position of missiles stored on central servers, is a very high priority for military operations. Thus, building quantum resilience ranks at the top of the agenda of the cyber branches of any national defense organization.
A technology that can help protect military communications and that has already been shown to work in 2018 relies on quantum mechanics: satellite QKD.[64] Even though the UK government is seeing the potential of QKD for securing critical communications,[65] this technology is of great interest to intelligence services. Research is performed, particularly in China, to investigate the issue from both perspectives: using QKD to encrypt own information and finding ways to obtain information if an adversary is applying QKD encryption.[66] Nevertheless, the IDA study also concludes that challenges such as authentication and the availability of secure non-quantum alternatives will prevent a breakthrough of QKD for military applications in the near future.[67]
Apart from studying QKD with respect to the opportunities it offers for secure communications and the threats it imposes on reconnaissance, the development of post-quantum cryptographic methods is also of relevance to the armed forces in order to provide communication channels and databases that are sufficiently safe to permit military operations in the quantum era.
Although it does not appear likely that quantum algorithms will ever be able to solve NP-complete problems in polynomial time, the speedup in solving TSP1 from S/2 computational steps required by classical computers down to S 1/2 steps facilitated by Grover’s quantum algorithm is significant. What effect on military operations could a future universal quantum computer with the ability to solve high-dimensional NP-complete problems with S 1/2 scaling have? The nature of TSP1 already indicates that Grover’s method may have an impact on military logistics. A quantum computer can possibly make navigation of tanks and support vehicles, warships, and aircraft a lot more efficient by optimizing routes connecting several military bases.
However, according to the IDA study, quantum optimization schemes such as Grover’s algorithm are not likely to achieve a sufficiently large advantage over classical heuristic approaches to play a substantial role, except for very large optimization problems.[68] In addition, quantum optimization using the Grover method requires FTQC and large quantum memory, which may be available only in the longer term.
Quantum annealers use a principle different from Grover’s algorithm to perform combinatorial optimization tasks, and some systems have already reached the commercial stage. The quantum advantage of these devices is still questioned, though.[69]
The game of chess essentially simulates a 6th-century Indian battlefield, and the ability to successfully play games of strategy like chess continues to be of great interest for the elaboration of military tactics. Chess or Go are games of a similar quality as TSP2, i.e., they represent PSPACE problems beyond the NP boundaries. The question of the performance of quantum algorithms in playing strategy games leads directly to QAI. In fact, chess has been a key model object of artificial intelligence since the origins of this field. Traditional chess programs are based on expert knowledge for the derivation of search and evaluation functions. The AlphaGo Zero chess program is an implementation of the idea of reinforcement learning, which is a sub-field of machine learning, which is a sub-field of artificial intelligence.[70] Without relying on input from chess masters, by reinforcement learning from self-play, AlphaGo Zero demonstrated in 2018 to be a game-changer by outperforming conventional chess programs.
This progress in “classical” artificial intelligence research suggests asking whether QAI, in particular quantum-enhanced machine learning, may provide another boost to strategy game computing. Recent investigations indicate that a realization of polynomial-time solutions to strategy games through quantum algorithms will not be possible. However, substantial accelerations as compared to classical algorithms still appear feasible, similar to the TSP1 scenario.[71]
The IDA study further points out that one main difficulty in quantum-enhanced machine learning is the need to deal with large training datasets.[72] Therefore, considerable advances in designing QRAM (the quantum equivalent of dynamic random access memory, DRAM) are necessary before realizations of QAI algorithms, e.g., for playing chess, are able to compete with classical machine learning implementations like AlphaGo Zero.
The scheme below illustrates, in the form of a hierarchical structure, how quantum computing may affect military interests. By defining four layers, which are differentiated according to increasing complexity, three sectors (cybersecurity, supply chain logistics, data analytics) of particular relevance to the military are identified. The graphic shows how the various sectors depend on applications like supervised machine learning and how the applications themselves are connected to core disciplines of quantum computing. Drug design and financial forecasts are just two examples of civilian sectors that will be changed by quantum computing.
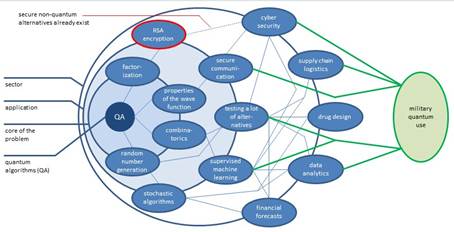 |
Figure 1: Potential Impact of Quantum Computing on Military Interests.
Figure 1 gives an idea of the impact quantum computing may have on selected branches of the military in graphical form. As discussed in this section, cybersecurity and supply chain logistics are sectors that are important for the armed forces and are at the same time very likely to be substantially transformed by developments in quantum computing. Data analytics is the third sector of interest to defense organizations, e.g., in the context of acquiring information on an opponent’s military activities, which is also particularly susceptible to advances in quantum algorithms. Reconnaissance satellites are collecting enormous amounts of data, and quantum computers, e.g., in the context of applications of QAI, may help extract valuable information.
VII. Summary
In Section II, we provided an overview of the scientific and technological background of quantum computer development, thus setting the basis for the discussion in the subsequent sections. Section III briefly presented prospective scenarios of quantum computing and, in particular, illustrated the difficulties complicating any predictions. Before considering specific implications of the quantum era on the military in Section VI, we first inserted a compact excursion into complexity theory (Section IV) to take a general look at the properties of quantum algorithms. Section IV’s remarks exclusively refer to future universal quantum computers since they presuppose the implementation of codes like those formulated by Shor and Grover. This leads to the investigation of the impact of future quantum devices on cybersecurity in Section V.
Experts disagree on the timeframe in which a universal quantum computer with the ability to, say, break RSA-2048 encryption using Shor’s algorithm will be available. This task requires the sustained entanglement of a larger number of qubits – an enormous technical challenge. Significant progress in fundamental and applied sciences will be necessary to build such a device, which involves significant uncertainty in providing a realistic perspective of quantum computing development. The US Government does not expect the commissioning of a quantum prime computer within the next several decades.
The forecasted power of such a computer to crack encryption keys is nevertheless of great interest to governmental organizations already now (cf. Section V). Quantum simulators as produced by D-Wave Systems, however, may have the ability to solve some optimization problems faster than classical computers and are already on the market. The high relevance of these quantum instruments to NATO is demonstrated by the fact that Lockheed Martin and Los Alamos National Laboratory are customers of D-Wave Systems.
The potentially high efficiency of quantum simulators in solving combinatorial optimization tasks makes them not only attractive for applications in the defense industry but also for deployments of military logistics. However, it is not yet clear whether these systems are providing a real quantum advantage.[73] NATO, therefore, should launch efforts to explore the risks and opportunities for its operations that are coming with quantum simulators.
The potential impact of quantum simulators on the two other sectors marked in Figure 1 as significant for the military, cybersecurity, and data analytics, is less obvious. However, these two sectors will experience massive transformations once a universal quantum computer reaches marketability.
Quantum computers able to compromise established cryptosystems may still be decades away, but NATO is nevertheless well advised to invest in the quantum resilience of its computer and network infrastructure. This can imply using full-entropy random numbers generated by quantum devices for encryption and employing longer keys for symmetric algorithms like AES. Long and fully randomized symmetric keys work for the wrapping of stored or replicated keys in order to make them quantum-safe. The crypto-agility of key managers implies their compatibility with longer keys and quantum-resistant algorithms. The replacement of the RSA protocol, e.g., by quantum-safe alternatives like lattice-based cryptography or SIDH, should be given priority. Also recommended is the implementation of secure links between management nodes via QKD and/or quantum-safe algorithms. Key exchange solutions such as QKD need to be also investigated with respect to their suitability for protecting long-distance communications.[74]
The employment of quantum computers to support tactical operations does not appear to be a near-term option since strategy games like chess correspond to PSPACE problems beyond the NP boundaries. However, the impressive chess-playing performance of the machine-learning application AlphaGo Zero demonstrates that QAI, as a particular quantum-enhanced machine learning, may play a role for the simulation of battlefield scenarios sooner than expected by many pundits, although necessary breakthroughs like in QRAM design still represent a major obstacle for the utilization of QAI.
Disclaimer
The views expressed are solely those of the author and do not represent official views of the PfP Consortium of Defense Academies and Security Studies Institutes, participating organizations, or the Consortium’s editors.
Acknowledgment
Connections: The Quarterly Journal, Vol. 20, 2021, is supported by the United States government.
About the Authors
Rupert Andreas Brandmeier studied economics (diploma) and archeology (BSc) at the Ludwig-Maximilian University (LMU), Munich. He obtained his Ph.D. degree with an analysis of the impacts of IT outsourcing. He is a Professor at the School of Management, Kutaisi International University.
E-mail: rupert.andreas.brandmeier@gmail.com
Jörn-Alexander Heye is a partner of JAM Systems Cyber Security Europe OÜ, Tallinn, Estonia, with over 28 years of international experience as a director and general manager. He is a German signal officer (reserve) in national and international deployments. E-mail: jheye@jamsys.eu
Clemens Woywod is a researcher for JAM Systems Cyber Security Europe OÜ in Munich. He is also affiliated with the chemistry department at the Technical University Munich. He earned a doctorate and a habilitation degree in theoretical chemistry from TU Munich. E-mail: clemens.woywod@ch.tum.de
20.030501.
- 8610 reads
- Google Scholar
- DOI
- RTF
- EndNote XML







